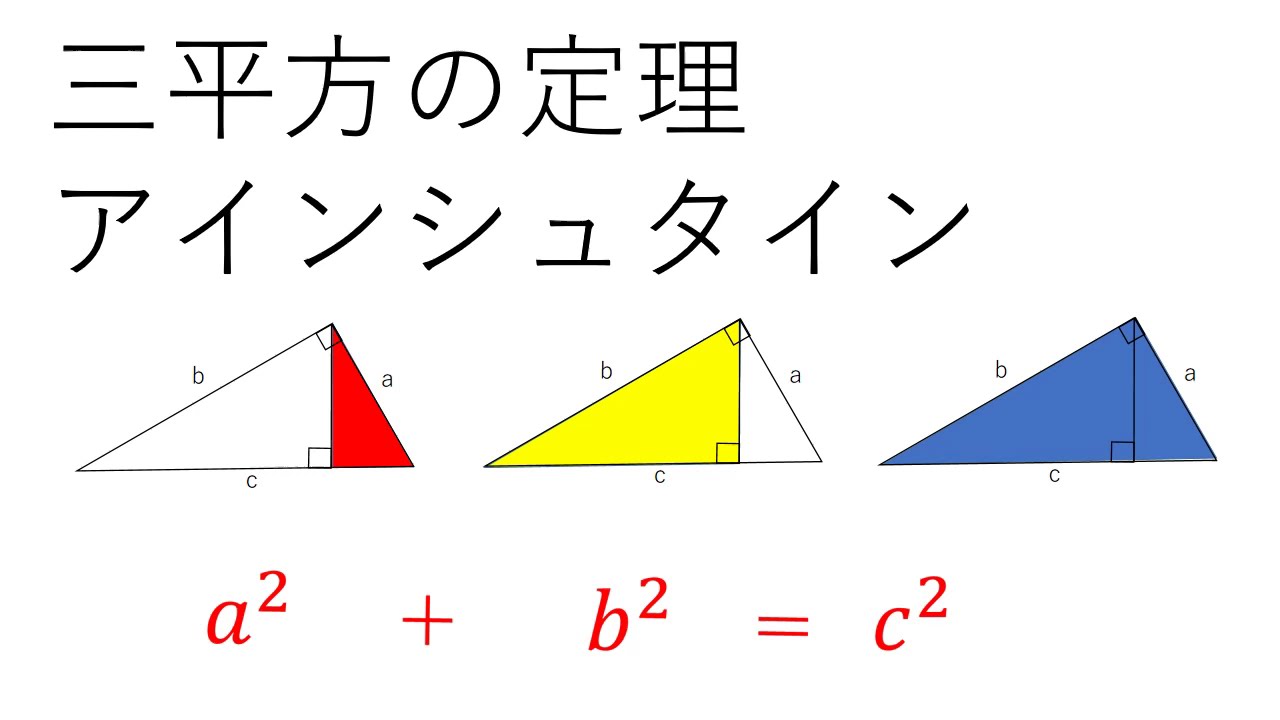
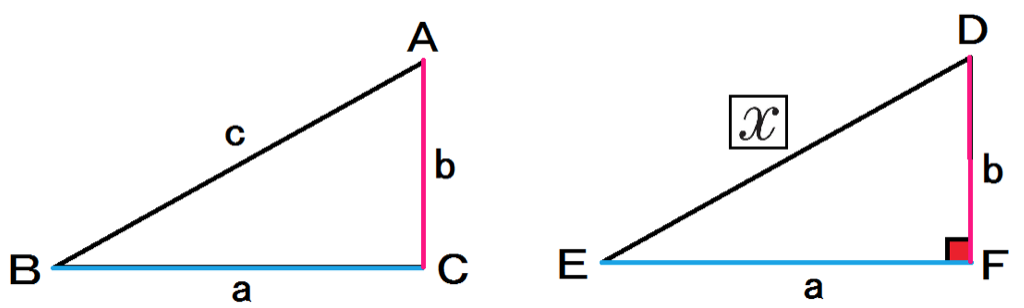
三平方の定理とは、直角三角形における各辺の長さに関する定理です。 証明したピタゴラスにちなんで、『ピタゴラスの定理』ともいわれます。 「斜辺(一番長い辺)の2乗」が、「他の辺の2乗の和」に等しいという定理です。 直角三角形の1辺の長さだけがわからない場合に、この定理を用いることで求めることができます。 また逆に、三角形の各辺について
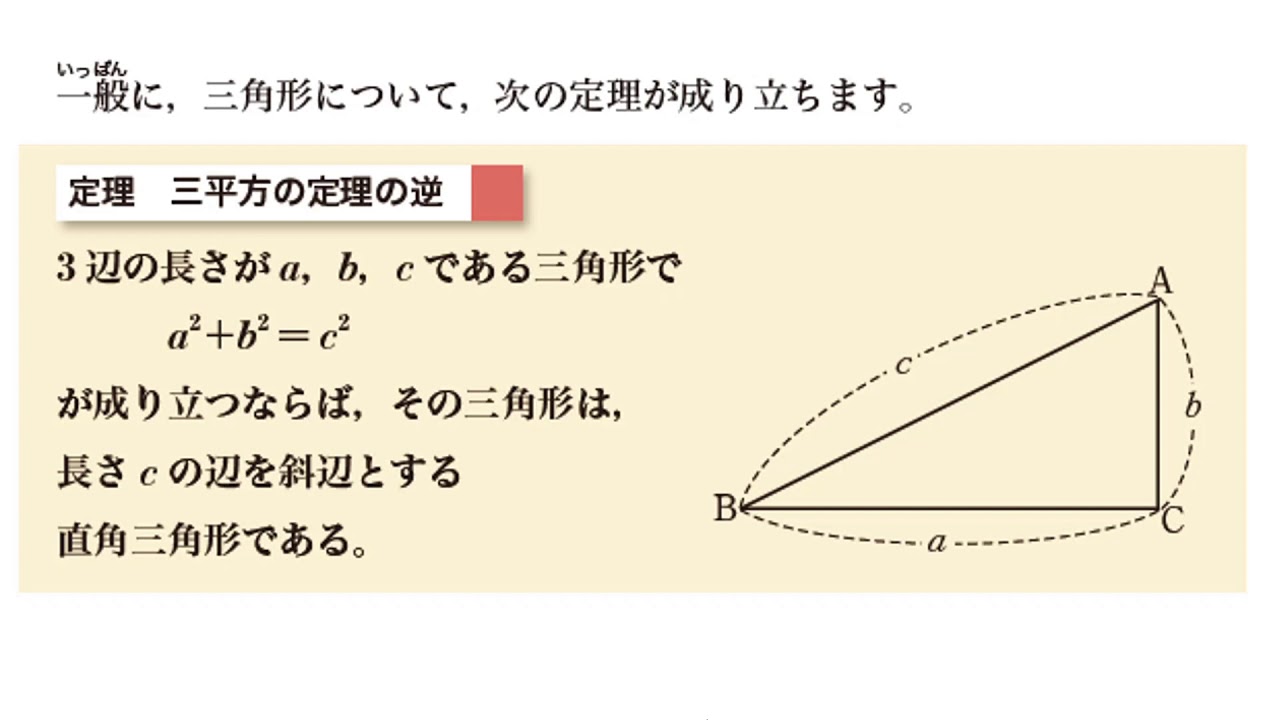
三平方の定理 証明 100-三平方の定理の逆まとめ お疲れ様でした! 三平方の定理の逆について理解していただけたでしょうか? これを使えば三角形の辺の長さから、その三角形が直角三角形になるかどうかを調べることができます。 証明などを問題として問われることは 回答 (3件中の1件目) 既に回答があるように, 三平方の定理は数多く知られています。しかし, 三平方の定理があまりにも基本的な性質なので, 変わった証明を考えるのは困難です。変わったことをしようとすると, 実は三平方の定理がなければ導けない事実を使ってしまうことがあるからです。
三平方の定理 証明 100のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 | ||
 |  | |
 | ||
「三平方の定理 証明 100」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  |  |
「三平方の定理 証明 100」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「三平方の定理 証明 100」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
 |  |  |
「三平方の定理 証明 100」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
 |  |  |
「三平方の定理 証明 100」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 |  | |
「三平方の定理 証明 100」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「三平方の定理 証明 100」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
 |  | |
「三平方の定理 証明 100」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |
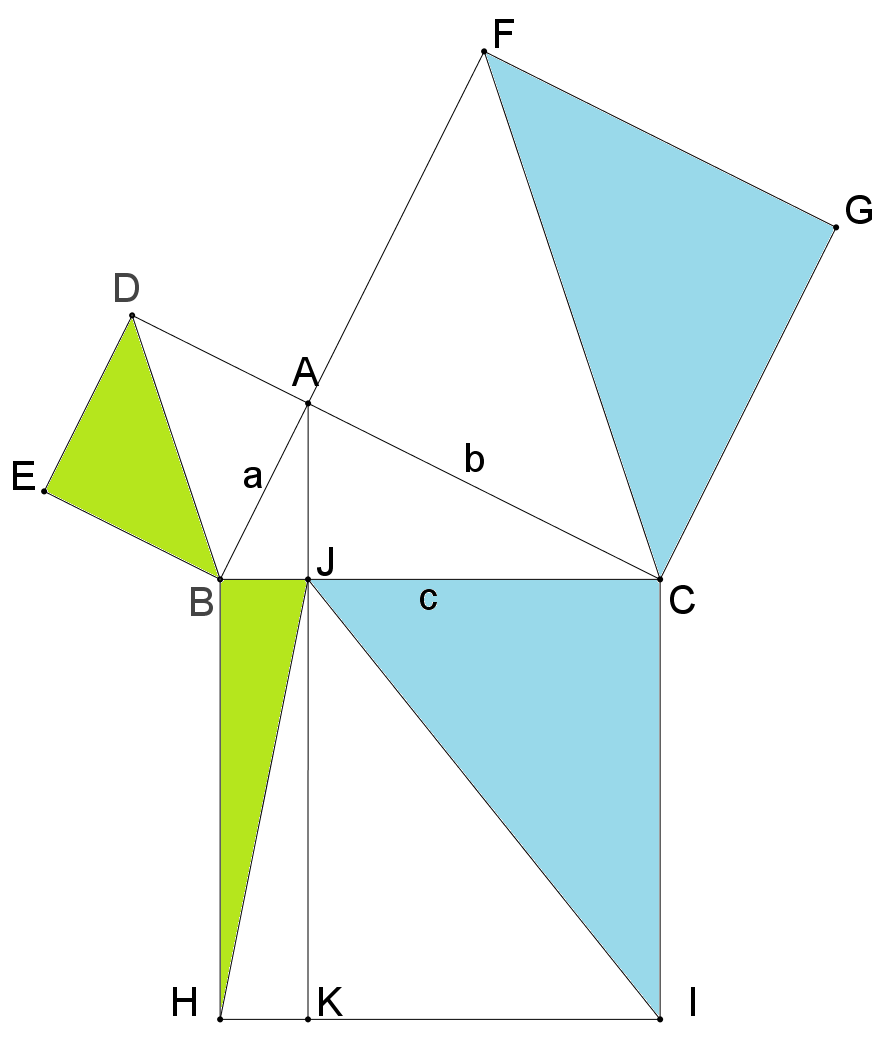
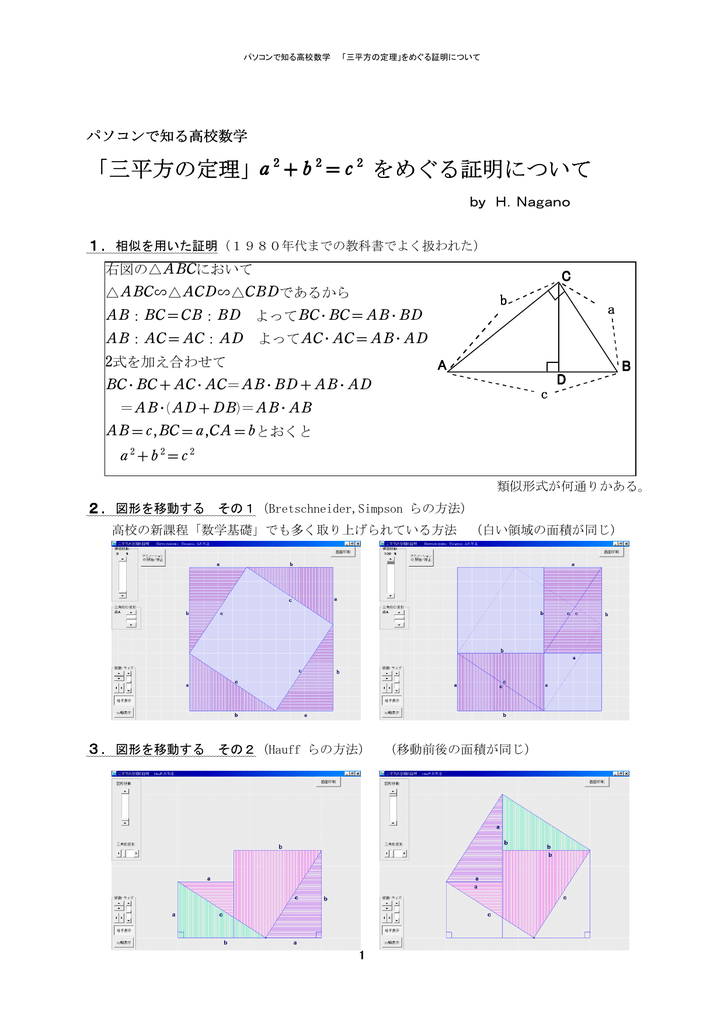
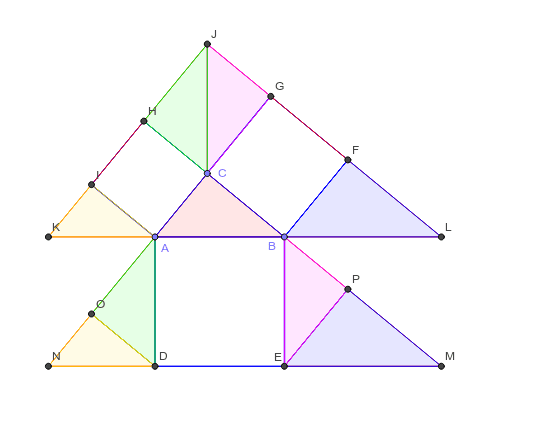
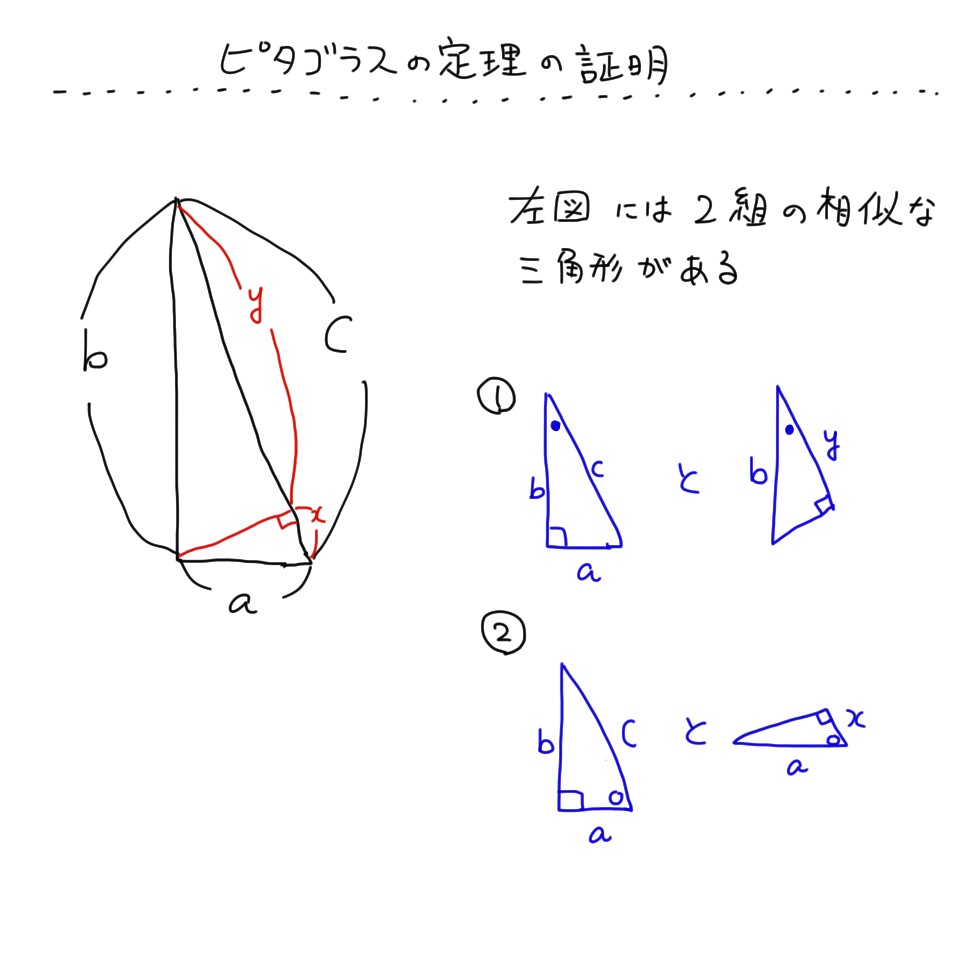
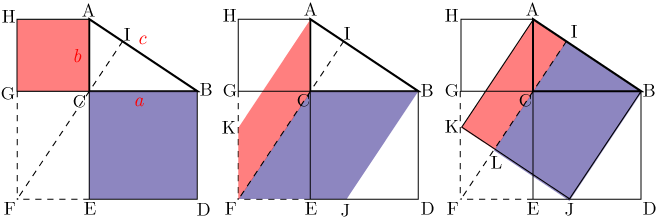
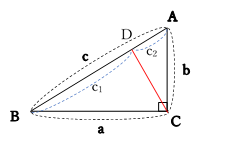
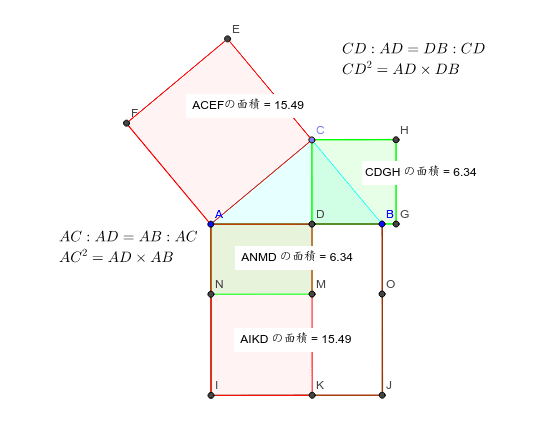
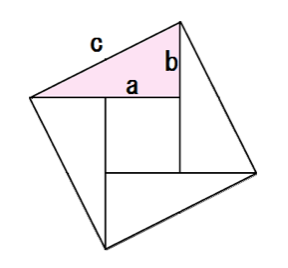
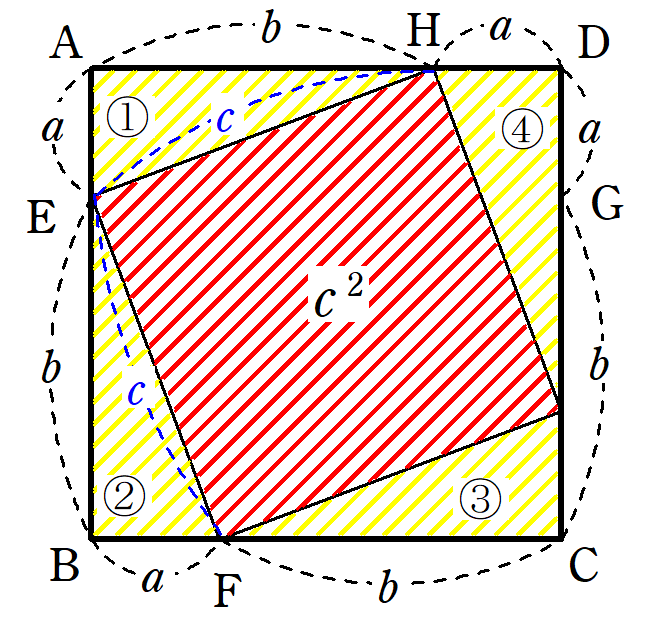
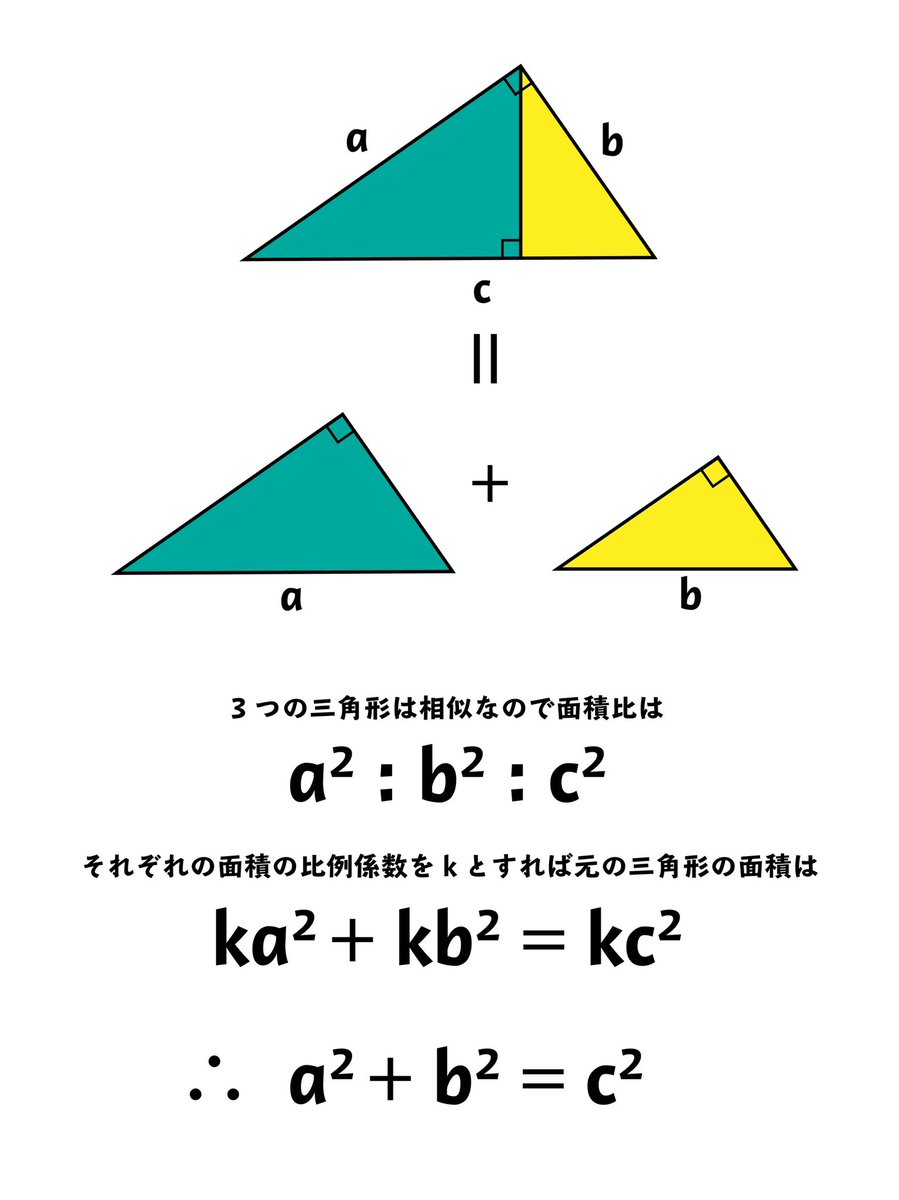
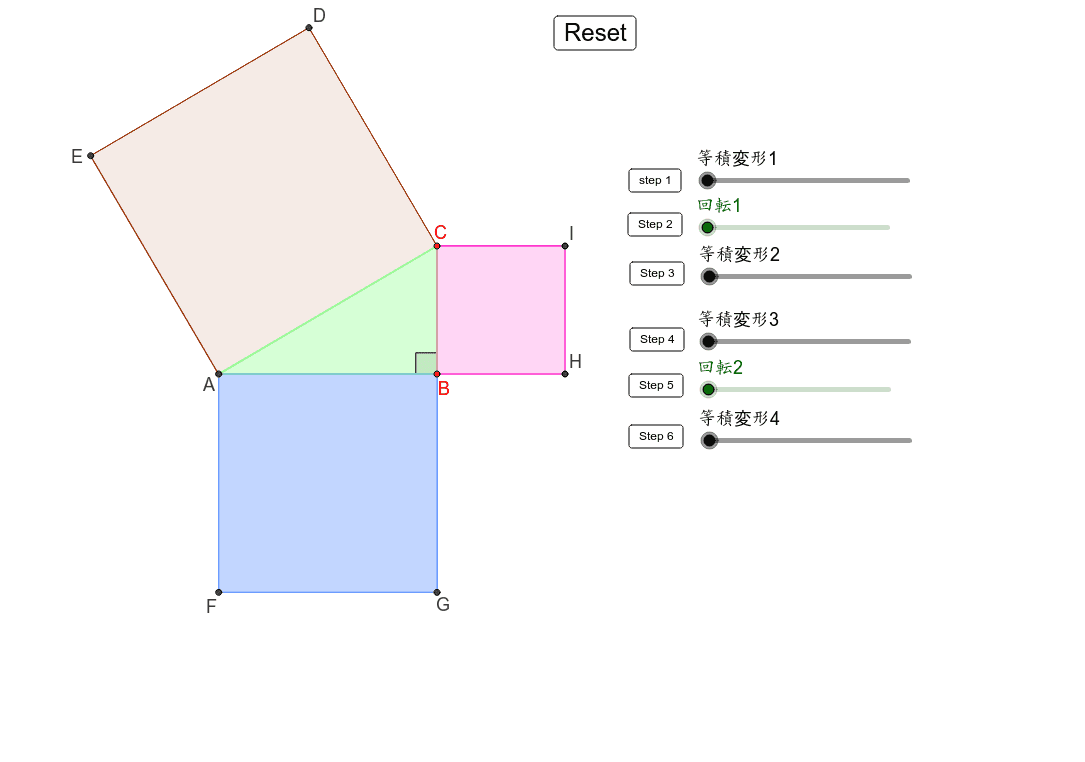
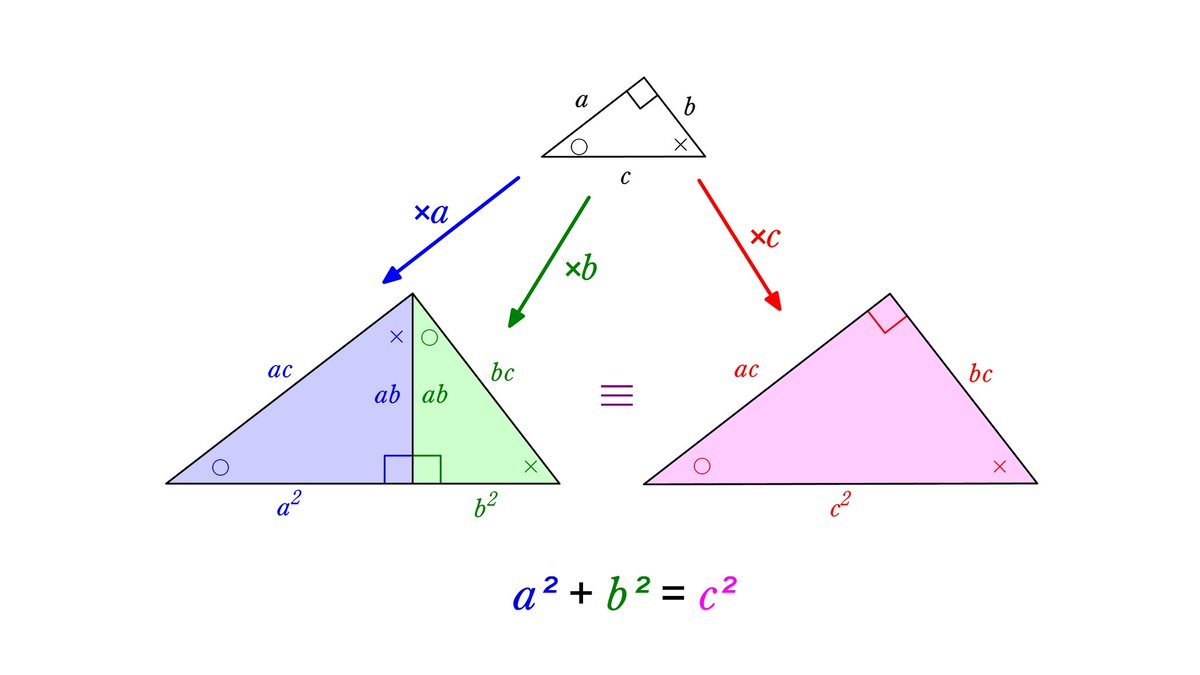
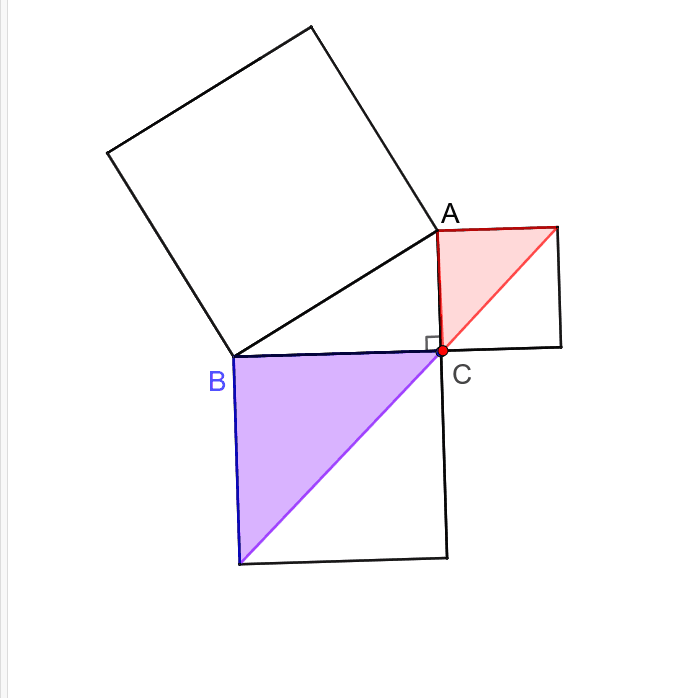
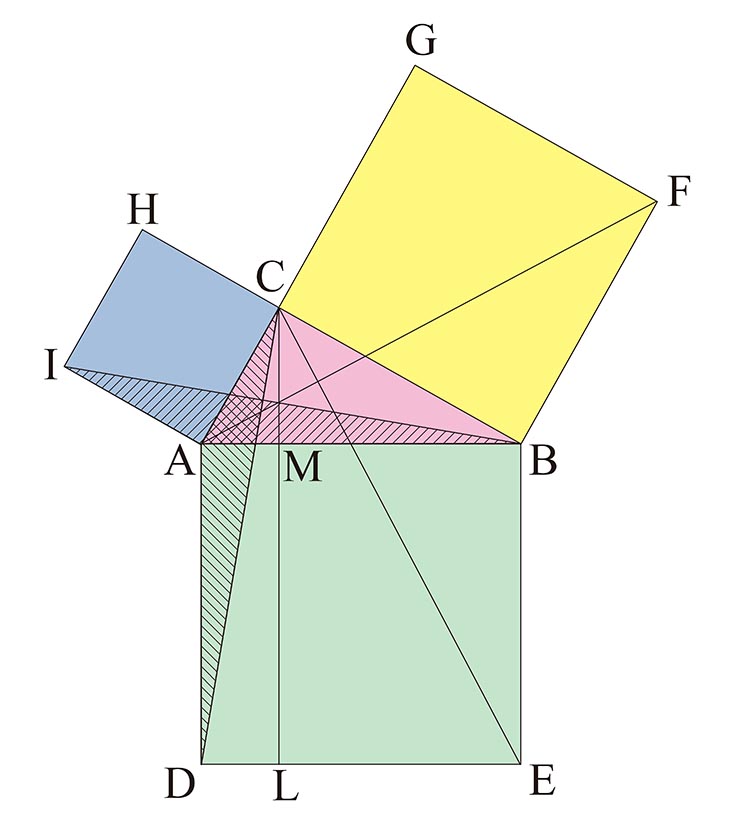
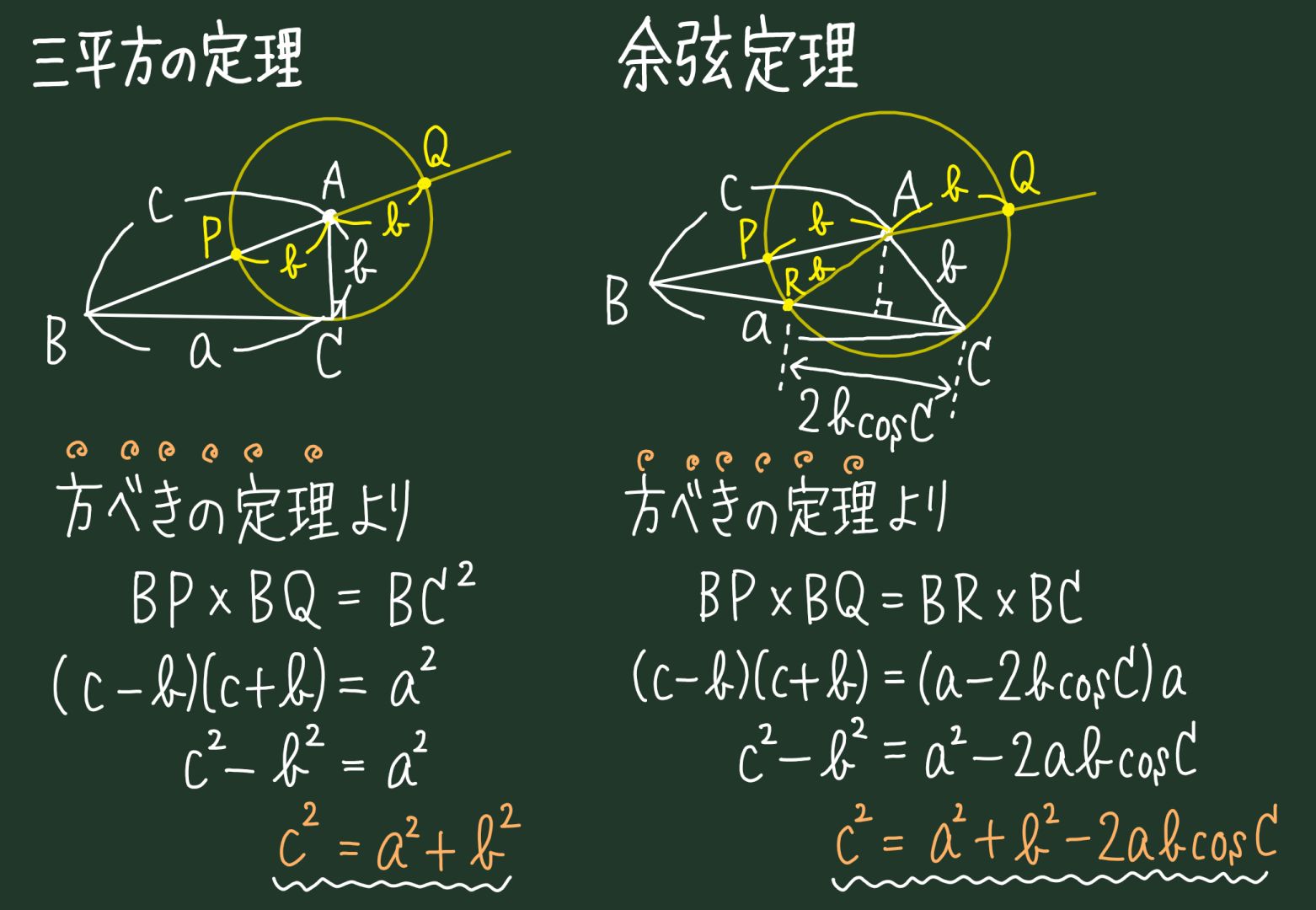
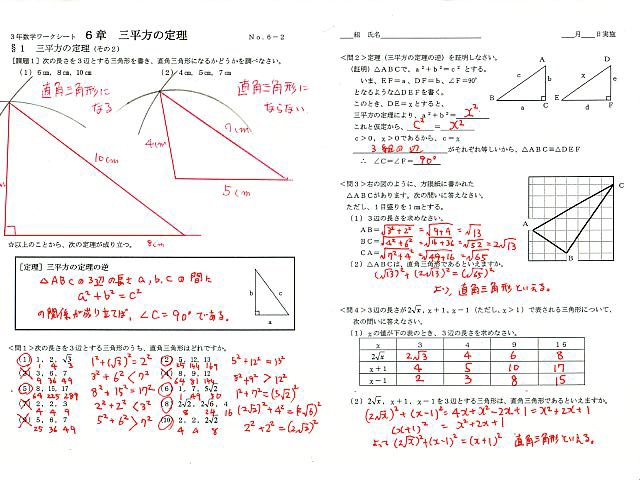
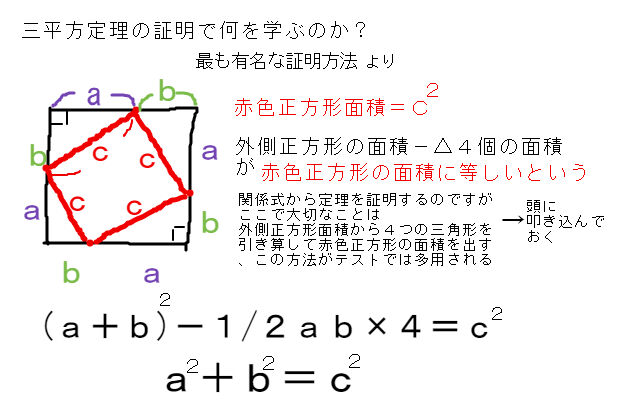
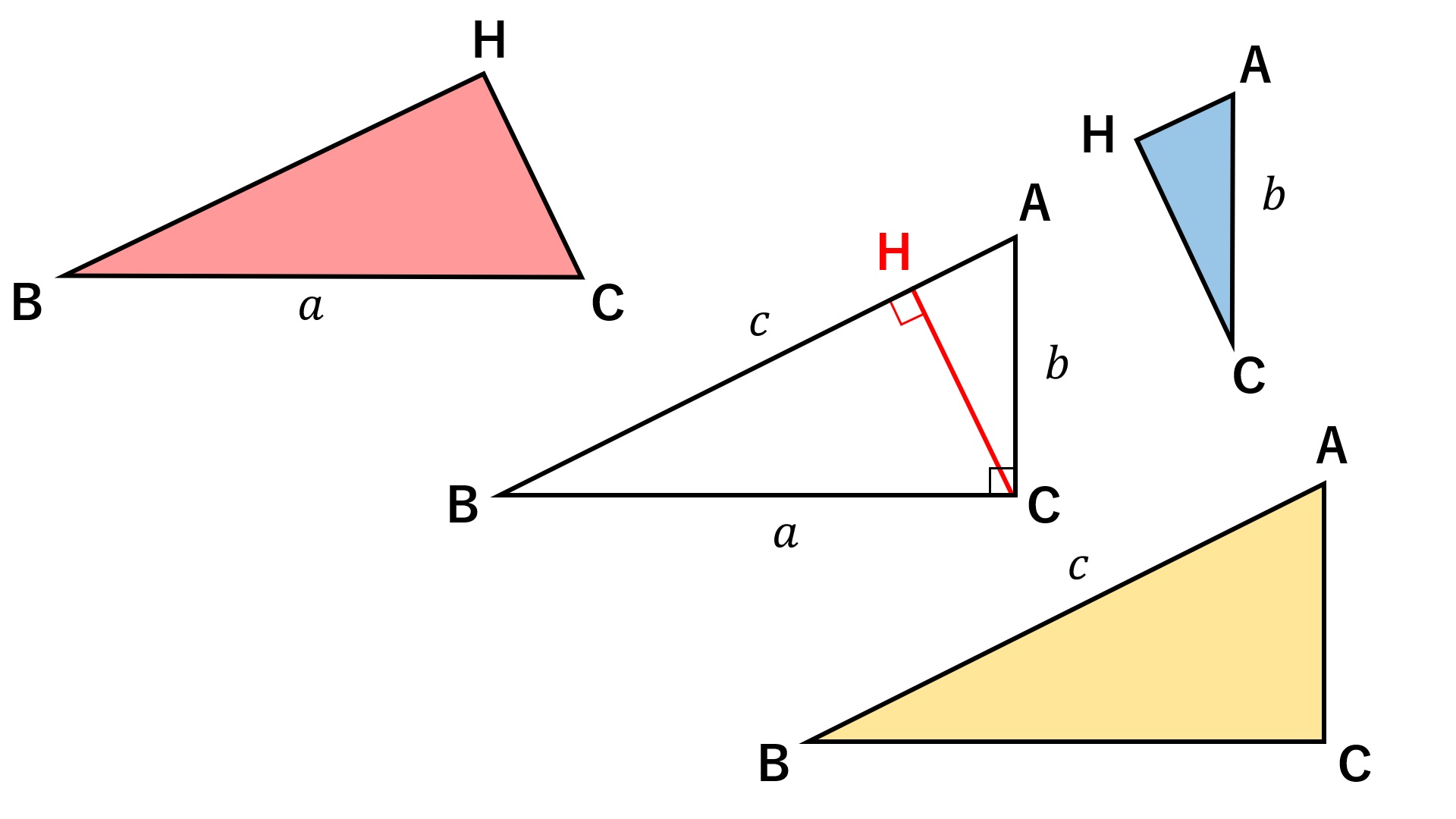
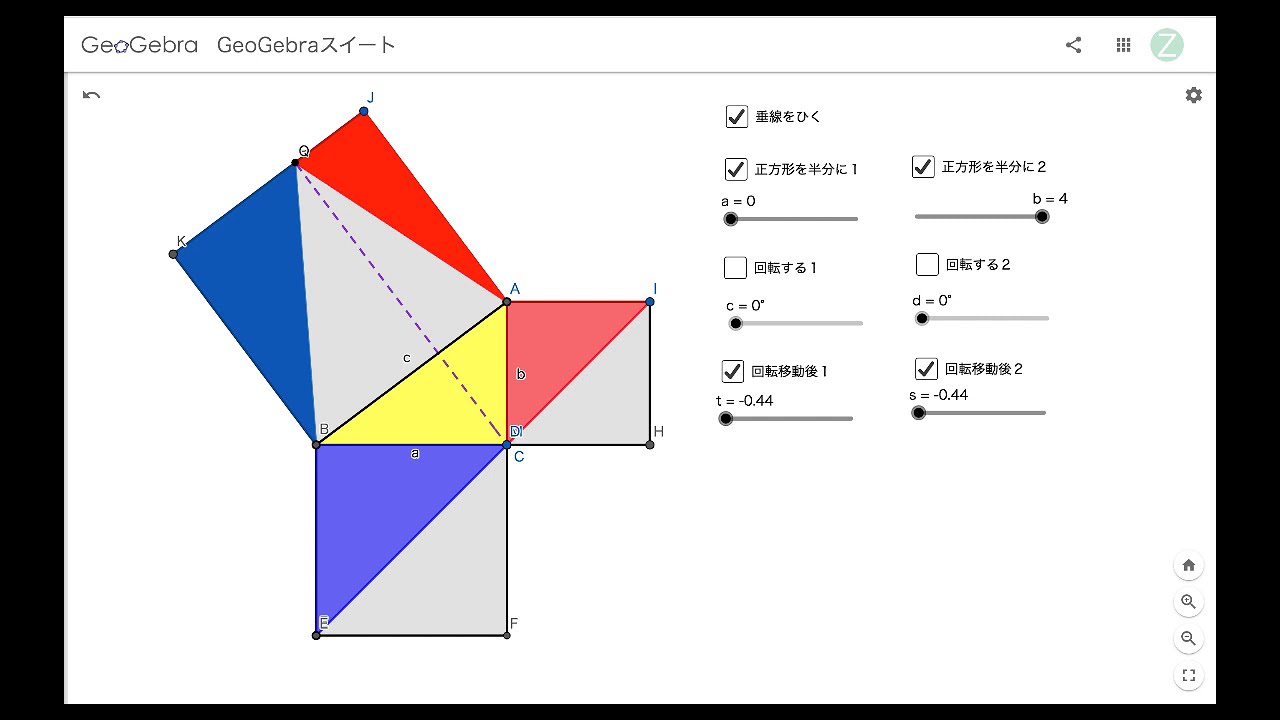
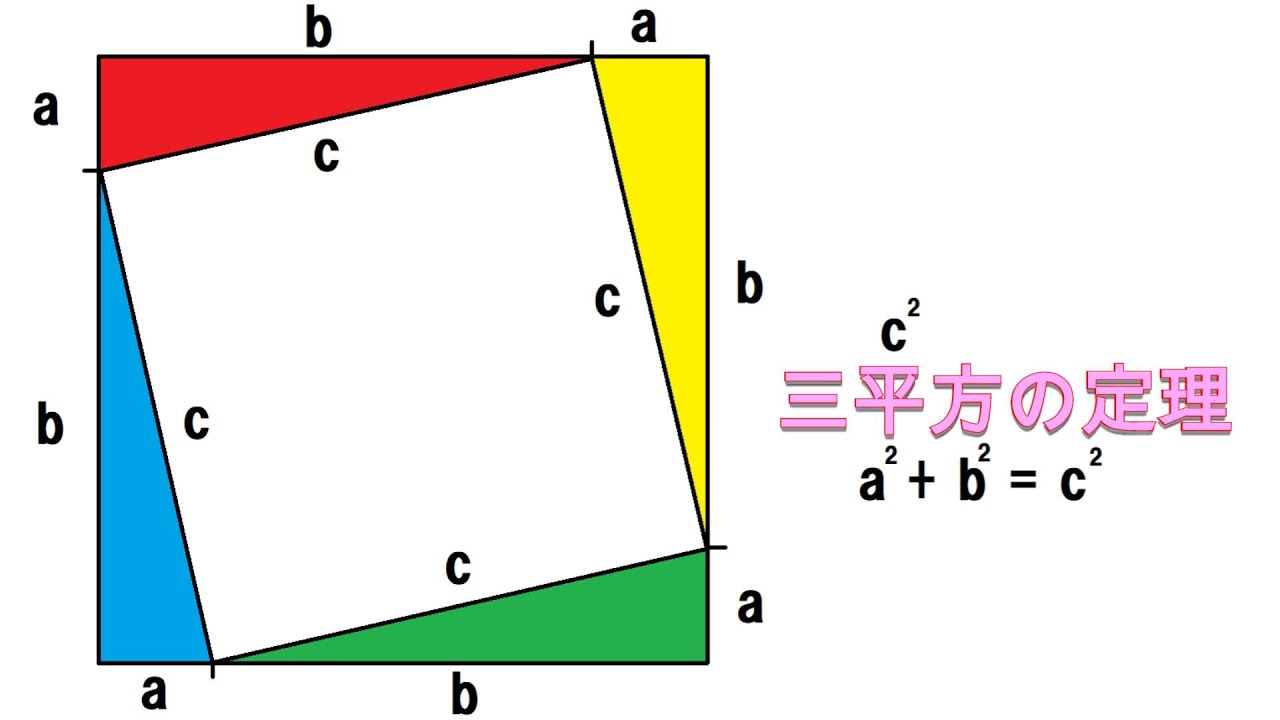
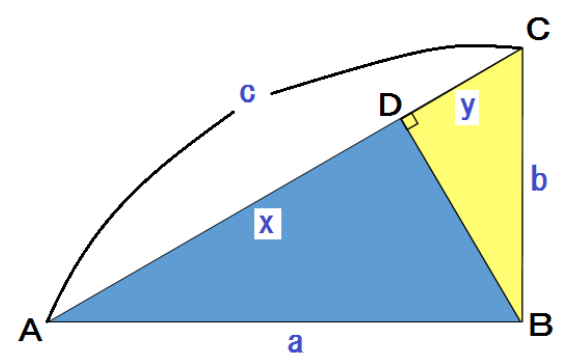
中学3年数学 三平方の定理 練習問題1・解答 中学3年数学 三平方の定理 練習問題1・解答1、次の問いに答えてください。 (1)次の図を利用して、a²+b²=c²であることを証明してください。 答え 証明 四角形ABCDは正方形で1辺がcですから、 面積 三平方の定理 証明 三平 代表的な三平方の定理の証明は「面積」を使うものが多く (たとえばユークリッドの等積変形を用いた証明)、 「面積」でなく「線分」の比で証明するフィボナッチのものは異色な感じがするので、取り上げました。 ポイントは線分比を使ってa, bそれぞれの2乗を作ること。 証明は以下
Incoming Term: 三平方の定理 証明, 三平方の定理 証明 中学生, 三平方の定理 証明 面白い, 三平方の定理 証明 一覧, 三平方の定理 証明 マイナー, 三平方の定理 証明 難しい, 三平方の定理 証明 相似, 三平方の定理 証明 中学生 簡単, 三平方の定理 証明 何通り, 三平方の定理 証明 100,




0 件のコメント:
コメントを投稿